5 Internals
5.1 The Math Bits
This section goes into detail on how Ruckus represents solid objects internally, which may help to explain why it behaves the way it does.
5.1.1 Implicit Surfaces and the Function Representation
In 3D graphics, surfaces are often represented explicitly by polygons along their boundary. This is not the only way to do it.
An implicit surface (Wikipedia) is a surface defined by the value of a field in space. By a "field," we mean a quantity that is measurable at every point in space. In the real world, the quantity might be density or electrical charge. Given a field, the implicit surface exists where the field is zero.
That was abstract. Let’s consider this in two dimensions. We can define a two-dimensional scalar field using an equation that maps X and Y to a number, such as:
(((sqr x) . + . (sqr y)) . - . 10)
We can graph this equation by using its result as a height level above the XY plane.
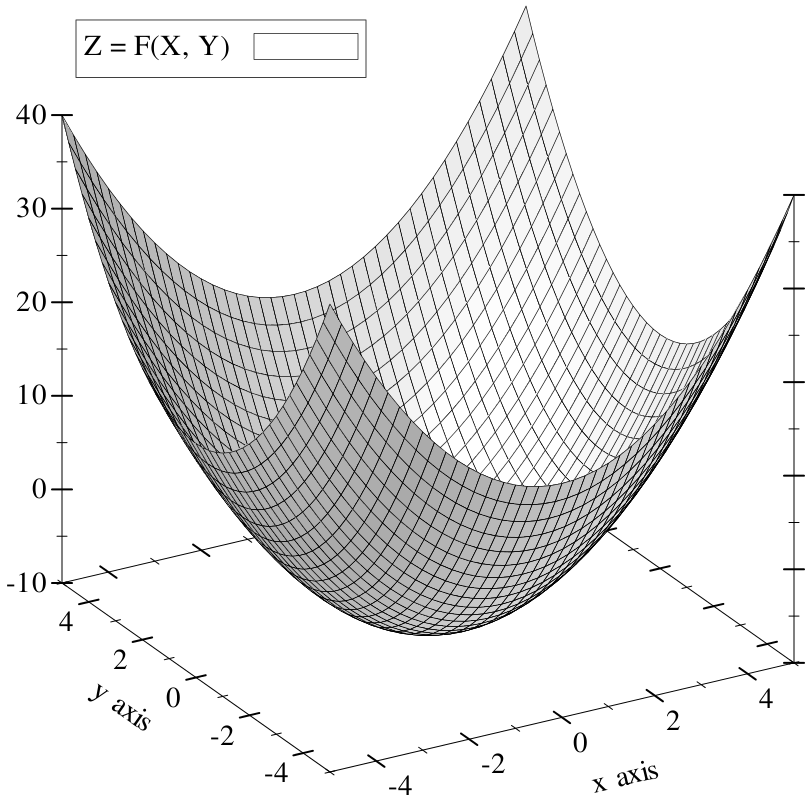
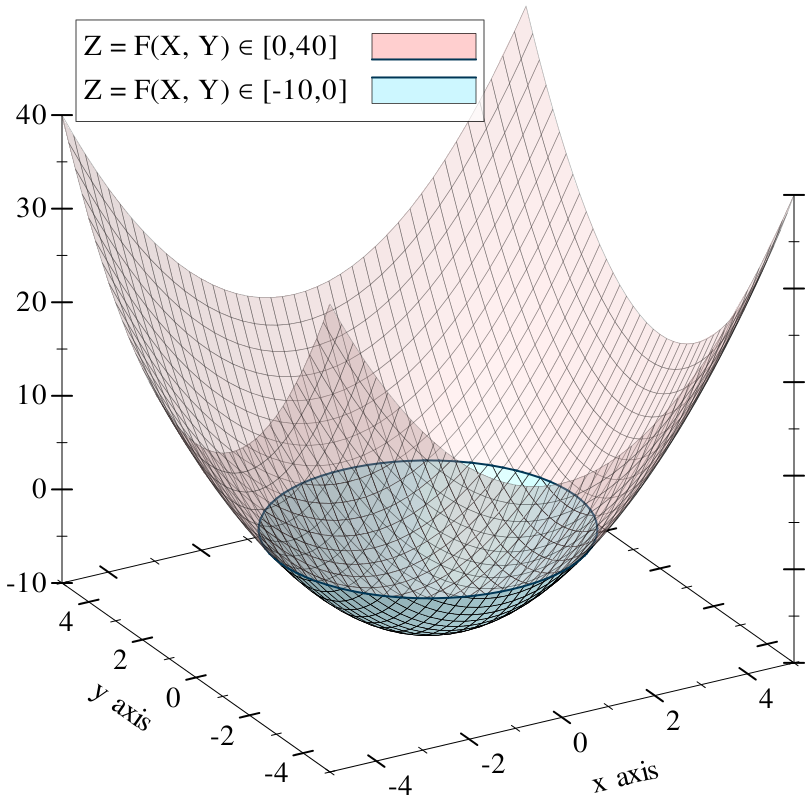
The heightfield intersects and dips beneath the XY plane in the center of the bowl shape:
The intersection of the heightfield with the XY plane is outlined in the plot above. This is the (infinite) set of XY points where our field level is zero. If we forgo the fancy 3D plot and draw these points on a Cartesian plane, we get a circle:
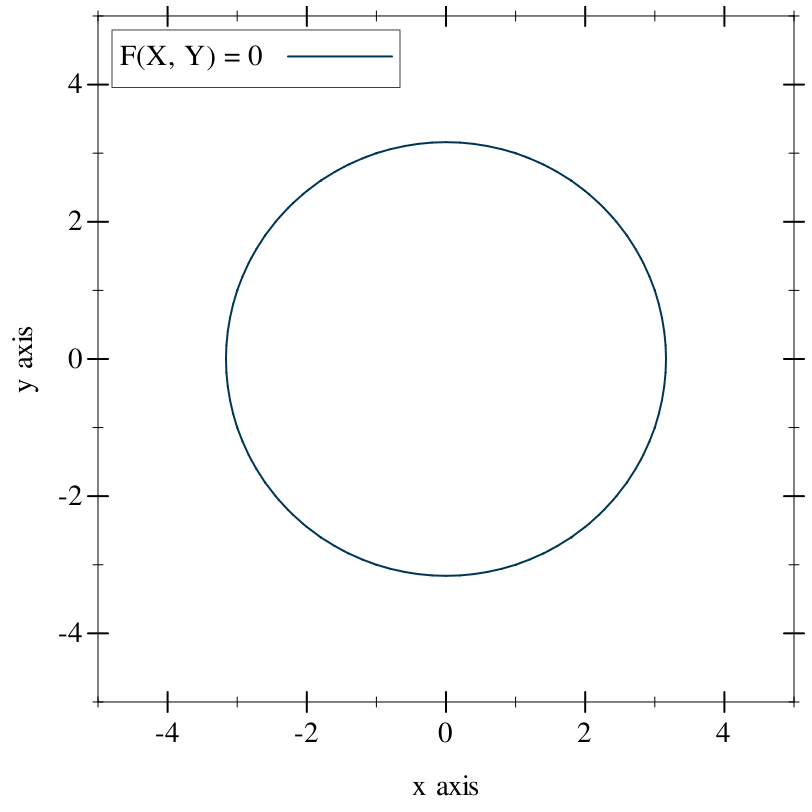
The set of points where the field is zero forms a two-dimensional implicit surface. One could even say that our equation is an implicit circle. This notion, that of identifying the equation with the surface it represents, is the function representation (Wikipedia), or f-rep. There are other representations of implicit surfaces, including data structures that directly describe geometric operations, or discretely sampled grids of field values.
Ruckus models solid objects using implicit surfaces in the function representation.
Because the objects are solid, they are not merely surfaces: they are oriented surfaces, with a distinct inside and outside. Specifically, Ruckus takes the perspective that any negative field value is "inside." This means that, in our running example, we have not just a circle but a solid disk:
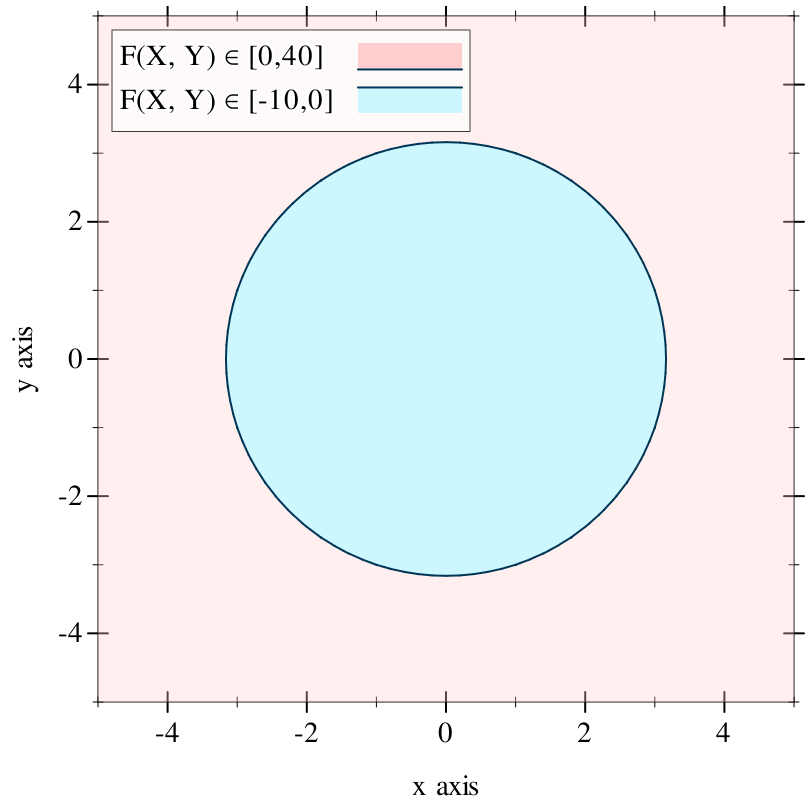
5.1.2 Signed Distance Fields
F-rep is interesting because it makes certain kinds of common operations on
shapes easier: intersection, subtraction, outsetting, filleting, and more. But
it isn’t all roses. It’s cheap to determine whether a given point is on the
surface of an f-rep object —
This class of traversal optimization for signed distance fields was first described, as far as I can tell, by John C. Hart in his paper Sphere tracing: a geometric method for the antialiased ray tracing of implicit surfaces (PDF).
This can be made cheaper for functions with certain characteristics. In
particular, there is a class of function called a signed distance
field that is a subset of the f-rep objects we’ve discussed so far. In a
signed distance field, the field value at a point not only indicates whether
the point is inside, outside, or on the surface of an object —
The equation we’ve been using so far is not a signed distance field, but we can alter it slightly so that it becomes one. Namely, we can make it into the Euclidean distance metric:
((sqrt ((sqr x) . + . (sqr y))) . - . 3)
This measures the length of the vector (x, y) using the Pythagorean theorem, and subtracts 3 so that the roots appear in a circle exactly three units away from the origin. It’s a circle with radius 3:
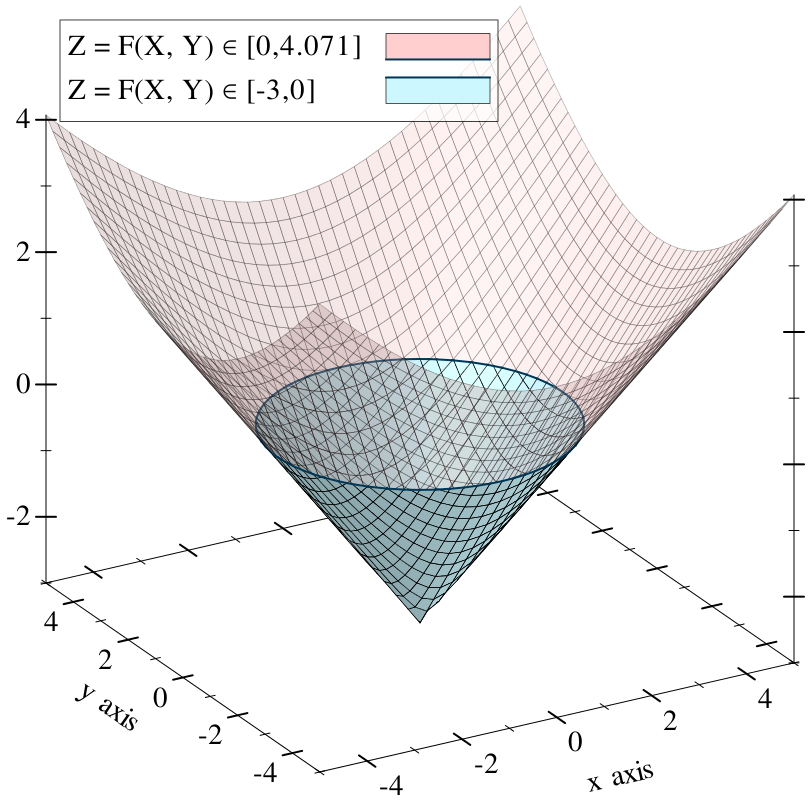
Compared to general f-rep implicit surfaces, signed distance fields allow for
some valuable optimizations. Sampling the field at any point gives the exact
distance to the nearest surface. If the field value is positive, one can infer
that there is no solid within a circle (in 2D) or sphere (3D) around the sample
point —
Iñigo Quilez has collected a wonderful menagerie of exact signed distance field functions for common primitives.
While it’s possible to analytically construct signed distance fields for many kinds of objects, it’s difficult to maintain a perfect distance field as objects are transformed, composed, or intersected. Certain apparently elementary transformations, such as scaling an object along only one axis, cannot be performed on a signed distance field f-rep solid.
So we have to loosen the rules a little.
5.1.3 The Lipschitz Criterion
Consider that a signed distance field works because we can predict its slope (the magnitude of its gradient vector). It’s exactly one: for every unit we move away from the surface, the field increases by one. This means we can assume that, given a field value v = F(x, y), there are no roots within v units in any direction of the point (x, y).
A bound on the slope of a field is known as the Lipschitz criterion (Wikipedia), and a function that is Lipschitz-continuous has a definite bound on its slope called its Lipschitz number. It’s usually written as a lowercase lambda (λ) but in the Ruckus sources, it’s written L.
A signed distance field has Lipschitz number 1. The optimization described above actually applies to any field with Lipschitz number between zero and one. It relies on the ability to derive an unbounding sphere for any point in space, so that it can skip forward with no risk of missing a surface. But it remains correct, if not quite as optimal, if we can only derive a conservative underestimate of the unbounding sphere. In other words, it’s okay if our unbounding spheres are wrong, as long as they’re too small rather than too large. Fields with this property are signed distance bound fields.
It is difficult to maintain a strict signed distance field under arbitrary transformations; it is much easier to maintain a definite Lipschitz number in a signed distance bound field. In Hart’s Sphere Tracing paper he presented a set of rules for maintaining Lipschitz continuity across transformations; more have since been discovered.
Ruckus represents solids as signed distance bound fields (0 < L <= 1).