6 Transformation

TODO: exposition about linear transformations and affine transformations

6.1 Basic Transformation Data Types

type
Linear
predicate
linear? : (-> Any Boolean : Linear)

The type and predicate for linear transformations.

procedure
(linear dx dy dz) → Linear
  dx : Dir
  dy : Dir
  dz : Dir

Converts three axes into a linear transformation.

procedure
(linear-x-axis t) → Dir
  t : Linear
procedure
(linear-y-axis t) → Dir
  t : Linear
procedure
(linear-z-axis t) → Dir
  t : Linear

Return the axes of t separately; i.e.

(match-define (linear dx dy dz) t)

is equivalent to

(define dx (linear-x-axis t))
(define dy (linear-y-axis t))
(define dz (linear-z-axis t))

value
identity-linear : Linear

The identity linear transformation: each axis is a coordinate axis.

Example:

> identity-linear
(linear +x +y +z)

procedure
(linear-compose t ...) → Linear
t : Linear

Composes any number of linear transformations. Applying the result applies each t once, in reverse order (just like compose).

procedure
(linear-inverse t) → Linear
t : Linear

Returns the inverse of the transformation t. Because Linear instances store their inverses, this operation is cheap.

If t isn’t invertible, linear-inverse raises an error. See linear-singular?.

procedure
(linear-singular? t) → Boolean
t : Linear

Returns #t when (linear-inverse t) would raise an error.

type
Affine
predicate
affine? : (-> Any Boolean : Affine)

The type and predicate for parallel-line-preserving transformations.

procedure
(affine dx dy dz p) → Affine
  dx : Dir
  dy : Dir
  dz : Dir
  p : Pos

Converts three axes and an origin into an affine transformation.

procedure
(affine-x-axis t) → Dir
  t : Affine
procedure
(affine-y-axis t) → Dir
  t : Affine
procedure
(affine-z-axis t) → Dir
  t : Affine
procedure
(affine-origin t) → Pos
  t : Affine

Return the axes and origin of t separately; i.e.

(match-define (affine dx dy dz p) t)

is equivalent to

(define dx (affine-x-axis t))
(define dy (affine-y-axis t))
(define dz (affine-z-axis t))
(define p (affine-origin t))

value
identity-affine : Affine

The identity affine transformation: each axis is a coordinate axis, and its origin is origin.

Examples:

> identity-affine
(linear +x +y +z)
> (affine-origin identity-affine)
origin

procedure
(affine-compose t ...) → Affine
t : Affine

Composes any number of affine transformations. Applying the result applies each t once, in reverse order (just like compose).

procedure
(affine-inverse t) → Affine
t : Affine

Returns the inverse of the transformation t. Because Affine instances store their inverses, this operation is cheap.

If t isn’t invertible, affine-inverse raises an error. See affine-singular?.

procedure
(affine-singular? t) → Boolean
t : Affine

Returns #t when (affine-inverse t) would raise an error.

procedure
(linear-consistent? t) → Boolean
t : Linear
procedure
(affine-consistent? t) → Boolean
t : Affine

Return #t when t preserves orientation, or handedness. An inconsistent transformation turns clockwise-oriented shapes or directions counterclockwise, and vice-versa.

Some 3D engines are sensitive to consistency: they will render shapes inside-out or turn normals the wrong direction when inconsistent transformations are applied. Pict3D’s rendering engine is not sensitive to consistency.

Examples:

> (define pict (cube origin 1/2))
> (define t (scale -1))
> (affine-consistent? t)
#f
> (transform pict t)

These functions are helpful for writing algorithms that preprocess geometric data in a consistency-insensitive way.

6.2 Transformation Combiners and Constructors

procedure
(transform pict t) → Pict3D
pict : Pict3D
t : Affine

Transforms pict by applying t.

Examples:

> (define pict (cube origin 1/2))
> (define t (affine-compose (move-z 1/4) (rotate-z 15)))
> (transform pict t)

procedure
(move pict dv) → Pict3D
  pict : Pict3D
  dv : Dir
procedure
(move-x pict dx) → Pict3D
  pict : Pict3D
  dx : Real
procedure
(move-y pict dy) → Pict3D
  pict : Pict3D
  dy : Real
procedure
(move-z pict dz) → Pict3D
  pict : Pict3D
  dz : Real

Move pict in direction dv, or along an axis dx, dy or dz units.

procedure
(move dv) → Affine
  dv : Dir
procedure
(move-x dx) → Affine
  dx : Real
procedure
(move-y dy) → Affine
  dy : Real
procedure
(move-z dz) → Affine
  dz : Real

Transformation-returning versions of the above. Any (move pict ...) is equivalent to (transform pict (move ...)).

procedure
(scale pict dv) → Pict3D
  pict : Pict3D
  dv : (U Real Dir)
procedure
(scale-x pict dx) → Pict3D
  pict : Pict3D
  dx : Real
procedure
(scale-y pict dy) → Pict3D
  pict : Pict3D
  dy : Real
procedure
(scale-z pict dz) → Pict3D
  pict : Pict3D
  dz : Real

Scales pict by dv, or by dx, dy or dz units along an axis. If dv is a real number d, it’s equivalent to (dir d d d) (i.e. uniform scaling).

The center of scaling—i.e. the only point that does not move—is the origin. This is often not what you want. To scale pict with a different center, see scale/center.

procedure
(scale dv) → Linear
  dv : (U Real Dir)
procedure
(scale-x dx) → Linear
  dx : Real
procedure
(scale-y dy) → Linear
  dy : Real
procedure
(scale-z dz) → Linear
  dz : Real

Transformation-returning versions of the above. Any (scale pict ...) is equivalent to (transform pict (scale ...)).

procedure
(rotate pict axis angle) → Pict3D
  pict : Pict3D
  axis : Dir
  angle : Real
procedure
(rotate-x pict angle) → Pict3D
  pict : Pict3D
  angle : Real
procedure
(rotate-y pict angle) → Pict3D
  pict : Pict3D
  angle : Real
procedure
(rotate-z pict angle) → Pict3D
  pict : Pict3D
  angle : Real

Rotate pict, angle degrees counterclockwise around axis, or around the +x, +y or +z axis.

The center of rotation is the origin. This is often not what you want. To rotate pict around a different center, see rotate/center.

procedure
(rotate axis angle) → Linear
  axis : Dir
  angle : Real
procedure
(rotate-x angle) → Linear
  angle : Real
procedure
(rotate-y angle) → Linear
  angle : Real
procedure
(rotate-z angle) → Linear
  angle : Real

Transformation-returning versions of the above. Any (rotate pict ...) is equivalent to (transform pict (rotate ...)).

procedure
(scale/center pict dv [v]) → Pict3D
  pict : Pict3D
  dv : (U Real Dir)
  v : Pos = (center pict)
procedure
(scale-x/center pict dx [v]) → Pict3D
  pict : Pict3D
  dx : Real
  v : Pos = (center pict)
procedure
(scale-y/center pict dy [v]) → Pict3D
  pict : Pict3D
  dy : Real
  v : Pos = (center pict)
procedure
(scale-z/center pict dz [v]) → Pict3D
  pict : Pict3D
  dz : Real
  v : Pos = (center pict)

Scales pict by dv, or by dx, dy or dz units along an axis, with center v.

By default, v is the center of pict’s bounding box. If pict doesn’t have a bounding box (for example, it’s the empty-pict3d), the origin is the default center.

(scale/center pict dv v) is implemented as

(local-transform pict (scale dv) (move (pos- v origin)))

In other words, pict is scaled in the local coordinate space of an axis-aligned basis with center v.

procedure
(rotate/center pict axis angle [v]) → Pict3D
  pict : Pict3D
  axis : Dir
  angle : Real
  v : Pos = (center pict)
procedure
(rotate-x/center pict angle [v]) → Pict3D
  pict : Pict3D
  angle : Real
  v : Pos = (center pict)
procedure
(rotate-y/center pict angle [v]) → Pict3D
  pict : Pict3D
  angle : Real
  v : Pos = (center pict)
procedure
(rotate-z/center pict angle [v]) → Pict3D
  pict : Pict3D
  angle : Real
  v : Pos = (center pict)

Rotate pict, angle degrees counterclockwise around axis, or around the +x, +y or +z axis, with center v.

By default, v is the center of pict’s bounding box. If pict doesn’t have a bounding box (for example, it’s the empty-pict3d), the origin is the default center.

(rotate/center pict axis angle v) is implemented as

(local-transform pict (rotate axis angle) (move (pos- v origin)))

In other words, pict is rotated in the local coordinate space of an axis-aligned basis with center v.

procedure
(point-at v
dv
[ #:angle angle
#:up up
#:normalize? normalize?]) → Affine
  v : Pos
  dv : Dir
  angle : Real = 0
  up : Dir = +z
  normalize? : Any = #t
(point-at v1
v2
[ #:angle angle
#:up up
#:normalize? normalize?]) → Affine
  v1 : Pos
  v2 : Pos
  angle : Real = 0
  up : Dir = +z
  normalize? : Any = #t

Returns a transformation that “points” from v in direction dv, or from v1 to v2.

More specifically, the z axis of the transformation points as described. If normalize? isn’t #f, the z axis has distance 1. Otherwise, dv or (pos- v2 v1) is used as the z axis directly.

The other axes always have distance 1, are perpendicular to the z axis and each other, and are rotated about the z axis angle degrees counterclockwise (viewing the z axis head-on). When angle is 0, the y axis points opposite up (i.e. downward), and the x axis points rightward. When the z axis is parallel to up, the rotation is arbitrary but always defined.

This function is really more intuitive than the above discription might suggest. It’s best used to place basis groups and cameras, and to stretch shapes between two points (see relocate).

procedure
(relocate t1 t2) → Affine
  t1 : Affine
  t2 : Affine
(relocate pict t1 t2) → Pict3D
  pict : Pict3D
  t1 : Affine
  t2 : Affine

Transforms pict from the local coordinate space defined by t1 into the local coordinate space defined by t2, or returns an Affine that does so.

For example, suppose we define a cylinder centered on the origin, and we want to stretch it between two arbitrary points.

> (define pict (with-color (rgba "red" 0.9)
(cylinder origin (dir 1/4 1/4 1/2))))
> (define pict-t (point-at (pos 0 0 -1/2) +z))
> (combine pict
(basis 'pict-t pict-t))

(We’re only using basis to visualize the transformation pict-t.) To stretch it between v1 and v2, we define a point-at transformation:

> (define v1 (pos 1 0 1))
> (define v2 (pos 0 1 1))
> (define new-t (point-at v1 v2 #:normalize? #f))
> (combine (sphere v1 0.2)
(sphere v2 0.2)
(basis 'new-t new-t))

Then we can use relocate to move pict into the new coordinate space:

> (combine (sphere v1 0.2)
(sphere v2 0.2)
(relocate pict pict-t new-t))

(relocate t1 t2) is implemented as

(affine-compose t2 (affine-inverse t1))

In other words, undo transformation t1, then do transformation t2.

procedure
(local-transform t local-t) → Affine
  t : Affine
  local-t : Affine
(local-transform pict t local-t) → Pict3D
  pict : Pict3D
  t : Affine
  local-t : Affine

Applies t to pict in the local coordinate space defined by local-t, or returns an Affine that does so.

(local-transform t local-t) is implemented as

(affine-compose local-t (relocate local-t t))

which is equivalent to

(affine-compose local-t t (affine-inverse local-t))

This operation is also known as a change of basis.

The scale/center and rotate/center functions are defined using local-transform, to apply scaling and rotating transformations in a local coordinate space with a center other than the origin.

procedure
(transform-pos v t) → Pos
  v : Pos
  t : Affine
procedure
(transform-dir dv t) → Dir
  dv : Dir
  t : Affine
procedure
(transform-norm dv t) → Dir
  dv : Dir
  t : Affine

Apply affine transformation t to a position, direction or normal.

The difference between applying a transformation to a direction and to a normal is best communicated with an extended example.

Examples:

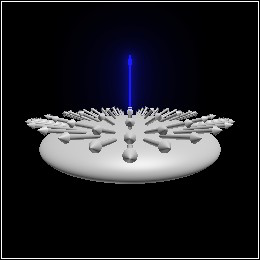
> (define pict (sphere origin 1))
> (define-values (vs dvs)
    (for*/lists (vs dvs) ([dx  (in-range -1 5/4 1/4)]
                          [dy  (in-range -1 5/4 1/4)])
      (define data (surface/data pict (dir dx dy 1)))
      (values (surface-data-pos data) (surface-data-normal data))))
> (combine
   pict
   (for/list ([v  (in-list vs)]
              [dv  (in-list dvs)])
     (arrow v (dir-scale dv 0.5))))
> (define t (scale-z 1/4))
> (combine
   (transform pict t)
   (for/list ([v  (in-list vs)]
              [dv  (in-list dvs)])
     (arrow (transform-pos v t)
            (dir-scale (transform-dir dv t) 0.5))))
> (combine
   (transform pict t)
   (for/list ([v  (in-list vs)]
              [dv  (in-list dvs)])
     (arrow (transform-pos v t)
            (dir-scale (transform-norm dv t) 0.5))))

In the second Pict3D, the directions have been flattened along with the sphere. In the third, they maintain their orthogonality to the surface.

procedure
(camera-transform pict) → (U #f Affine)
pict : Pict3D

Returns the camera used to orient the initial view, if at least one 'camera basis is in pict. If there are none, returns #f.

procedure
(camera-ray-dir t
[ #:width width
#:height height
#:z-near z-near
#:z-far z-far
#:fov fov]) → (-> Real Real Dir)
  t : Affine
  width : Integer = (current-pict3d-width)
  height : Integer = (current-pict3d-height)
  z-near : Real = (current-pict3d-z-near)
  z-far : Real = (current-pict3d-z-far)
  fov : Real = (current-pict3d-fov)

Creates a function that accepts screen coordinates and returns the direction of the ray from the camera’s origin to those coordinates in the camera’s local coordinate space.

If (<= 0 x width) and (<= 0 y height), then the position (pos+ (affine-origin t) ((camera-ray-dir t) x y)) lies on the z-near plane.

A common use of camera-ray-dir is to find objects under a mouse cursor in a rendered Pict3D.

A less common use is to build a ray tracer in very few lines of code, such as the following.

> (define p (combine
             (cube origin 1/2)
             (for*/list ([i  (in-range -1 2)]
                         [j  (in-range -1 2)]
                         [k  (in-range -1 2)])
               (sphere (pos (* 0.35 i) (* 0.35 j) (* 0.35 k)) 0.2))))
> p
> (define t ((current-pict3d-auto-camera) p))
> (define v0 (affine-origin t))
> (define ray-dir (camera-ray-dir t))
> (define l (pos 1.0 1.5 2.0))
> (require images/flomap)
> (flomap->bitmap
   (build-flomap
    1 (current-pict3d-width) (current-pict3d-height)
    ; for each screen coordinate on a grayscale surface...
    (λ (_ x y)
      ; trace from the camera origin through the screen at x,y
      (define-values (v n) (trace/normal p v0 (ray-dir (+ x 0.5) (+ y 0.5))))
      (cond [(and v n)
             ; direction from surface point to light source
             (define dl (pos- l v))
             ; distance squared to light source
             (define m^2 (dir-dist^2 dl))
             ; 3.0 brightness, inverse-square attenuation
             (define a (/ 3.0 m^2))
             ; Lambert's cosine law (fully diffuse material)
             (define b (max 0.0 (/ (dir-dot n dl) (sqrt m^2))))
             ; compute brightness, apply gamma correction
             (expt (* a b) (/ 1.0 2.2))]
            [else  0.0]))))

top ← prev up next →

1	Quick Start
2	Constructors
3	Shape Attributes
4	Position and Direction Vectors
5	Combining Scenes
6	Transformation
7	Deformation and Tessellation
8	Collision Detection
9	Rendering
10	3D Universe

6.1	Basic Transformation Data Types
6.2	Transformation Combiners and Constructors