7 Deformation and Tessellation
TODO: exposition about deformation and tessellation and Jacobian
7.1 Basic Deformation Data Types
The type and predicate for three-dimensional, almost-everywhere continuously differentiable
functions.
This includes
Affine (and thus
Linear) as a subtype.
Creates a deformation function. If only
f is given, it is numerically differentiated to
construct the
Jacobian function. Otherwise,
j is used.
Warning: If f is numerically differentiated, it may be evaluated outside of its
intended domain.
Return the function represented by
t and its
Jacobian matrix of partial derivatives.
When t is Linear or Affine, (smooth-function t) is equivalent to
(λ (v) (transform-pos v t)).
When t is Linear, (smooth-jacobian t) is equivalent to (λ (_) t).
Composes any number of
deformations.
Applying the result applies each
t once, in reverse order (just like
compose).
Example:
Returns the best linear approximation of t at point v.
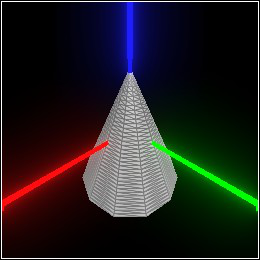
7.2 Tessellation
Approximates
pict with triangles so
deformations can be applied to their vertices.
Each kind of shape has its own tessellation algorithm, which follows the these general guidelines:
When
max-edge is
#f (the default), it’s computed as
(/ l segments), where
l is the length of the longest axis of
pict’s bounding rectangle.
Examples:
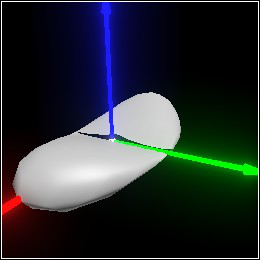
Tries to tessellate
pict in a way that reduces visual artifacts when deformed by
t.
This function is available for completeness; usually
adaptive-deform is more appropriate.
Examples:
Requests an initial tessellation of each shape with max-angle = 90 and
max-edge = +inf.0.
For up to max-iters iterations, splits triangle edges that, when transformed,
would be too long or represent too many degrees of an arc, and moves the new vertex onto the
shape’s surface.
For up to 3 iterations, splits triangle edges that change orientation when transformed,
using flbracketed-root to solve for locations at which t’s
Jacobian determinant is zero.
This is a lot of extra work, which usually can’t be done at interactive speeds.
On the other hand,
adaptive-tessellate sometimes uses fewer triangles (this is still a
work in progress), and can deal better with deformations with discontinuities and local
noninvertibility.
Examples:
7.3 Deformation Constructors and Combiners
Apply
deformation t to a position, direction or normal.
These are analogous to transform-pos, transform-dir and transform-norm,
respectively.
(In fact, when t is Affine, they simply apply their affine counterparts.)
The main difference is that deform-dir and deform-norm require a position
argument to apply the Jacobian to.
Group transformations, and untessellated solid objects such as spheres, are deformed
using deform-affine.
Deforms pict by applying t to its positions, normals and affine transformations.
Tries to tessellate
pict in a way that reduces visual artifacts when deformed by
t,
and then deforms the tessellation by
t.
See
adaptive-tessellate for discussion and examples.
Applies
t to
pict in the local coordinate space defined by
local-t, or
returns a
Smooth function that does so. Analogous to
local-transform.
The two-argument version is equivalent to
(smooth-compose local-t t (affine-inverse local-t)).
In English, undo local-t, do t, then redo local-t.
Twists pict around the z axis, angle degrees per unit height.
In the above example, the pipe is twisted 180 degrees: 90 degrees for one unit below the origin,
and 90 degrees for one unit above the origin.
Adds (f x y) to every point’s z coordinate in pict.
Bends pict by bending an interval of the z axis angle degrees
counterclockwise around the y axis.
If zrange is given, only that interval on the z axis is bent; otherwise,
the entire z extent of pict is used.
The bent interval always retains its length.
Example:
Deformation-returning versions of the above.
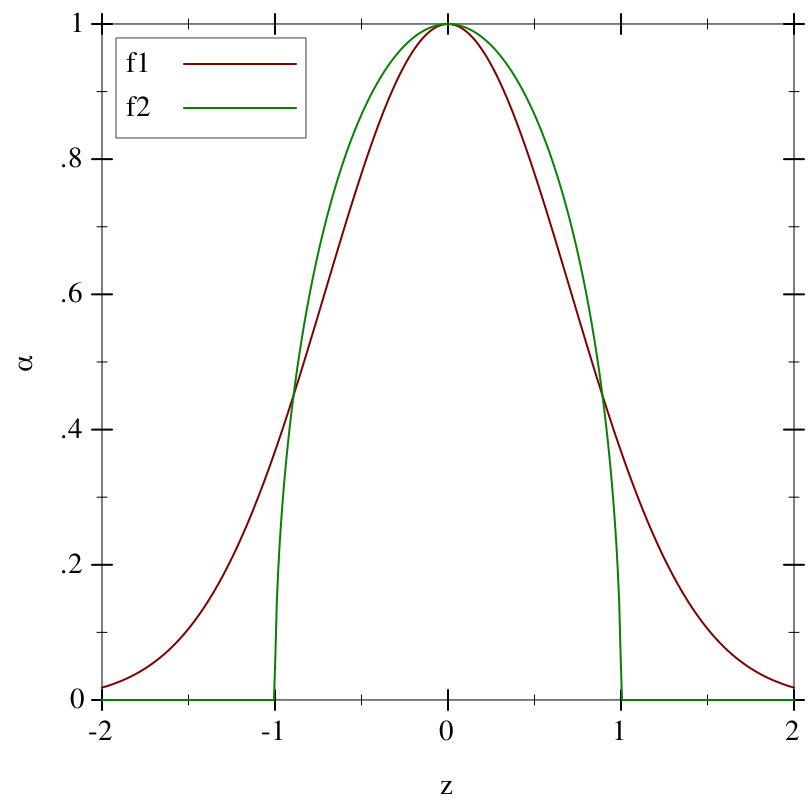
Returns an average of t1 and t2, weighted by α.
When α is a function, the weight at each point v is (α v).